Task estimation: Conquering Hofstadter's Law
How to turn your estimates into reliable predictions — and communicate them.
Estimating the completion time of tasks is important work. It’s also something that brings great anguish to a lot of engineers and software developers, and causes significant friction between dev teams, management, other departments, and customers.
This is because almost everybody is still talking about estimation the wrong way.
Below is a true story.1
An experienced team of developers was tasked with a full ground-up, from-scratch rewrite of a mature software stack that had been built over many years of development. The legacy architecture had been stretched to its limits and was now restricting the company's growth. A complete redesign was needed; backwards-compatible on the surface, but entirely different under the hood. Everyone knew this would be a difficult undertaking, but the team had thoroughly considered all the alternatives, and decided this was the best way forward.
Marketing wanted to know when the new software would be ready to ship. The dev team put together a roadmap to deliver a minimum viable product, planned out the workload, and estimated how long it would take to get to the MVP: six months.
It shipped two years later.
Hofstadter's Law: It always takes longer than you expect, even when you take into account Hofstadter's Law.
— Douglas Hofstadter
It would be an understatement to say this was a huge problem. But the problem wasn't the two years of development time; this company had healthy revenue to go on, and the long-term payoff from the technology leap would eventually be worth that incubation period.
The damage was caused by the estimate itself. You see, the marketing team interpreted this estimate as a commitment, and began informing customers about when the product would be ready. Sales inquiries came streaming in. Some of those customers had customers of their own, and they had started making their own plans and timelines based on this information. When the deadline rolled around and the product was nowhere near ready, there was a lot of damage control needed.
Customers were not happy. The marketing team was not happy. The company was not happy. And the dev team found themselves in the crosshairs.
So what went wrong?
I want to be very clear about this: this team was fantastically skilled, productive, well-managed and effective. These are among the most talented developers I have ever met, and together they were a well-oiled machine, outperforming the sum of their parts. I doubt anyone could have done the job faster or better.
If you have experience with projects that run behind schedule, you are likely thinking “scope creep” (a pathology where new deliverables are added throughout a project, extending the timeline beyond the original estimate). And yes, that was a factor, although I think a more accurate term in this case would be “scope discovery”. The project set out to lay a forward-looking foundation to satisfy future needs, and some learning happened along the way. That's always the case in the tech industry.
I already mentioned that the devs thought they were offering a guess, while the marketing team thought they were hearing a commitment; clarifying that language company-wide was the first step toward restoring trust. But the deeper problem was that nobody on either side properly understood how to account for the uncertainty in these estimates, not even the developers themselves.
Spotting a pattern
If you work in the tech industry, this story probably sounds very familiar to you. A timeline estimate gets missed by a factor of [TOO_MUCH], the dev team ends up in hot water, and stressed-out engineers end up working crunch time to make ends meet.
This happens despite all kinds of tricks and practices teams use to make estimates work better: Fibonacci numbers. Story points. Planning poker. Gantt charts. Retrospectives. None of these are able to conquer the horror that is Hosftadter's law. I've even seen teams give up on estimating altogether as some hopeless, Dilbert-style exercise. Have faith!
So here's where the story takes a turn. This was an existential crisis for the team, and they responded in the best way possible: seizing the opportunity to raise the level of their game.
Feeling a bit shaken, the team set out to improve their estimates scientifically. The team began gathering data, possibly the most accurate and fine-grained data of this sort that any company has ever gathered, comparing their prior estimates with actual outcomes. I cannot share that data with you,2 but I can explain the clear pattern that emerged.
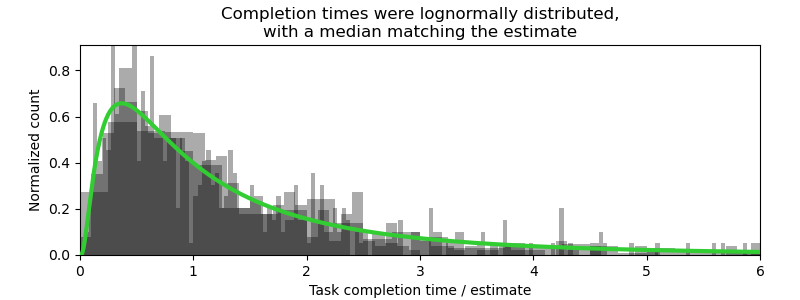
If we were to gather all the tasks that were estimated at 2 hours, their measured completion times looked very much like this:
If we were to do the same for tasks estimated at 5 hours, the plot looked like this:
For 13 hours? Like this:
Does anything jump out at you?
The first thing that jumped out to the team was a lot of two-hour tasks that took ten hours to finish. The average was also optimistic by a factor of about 1.6, putting the sprints constantly behind schedule.3 Seeing just how far off their estimates were was quite a disappointing result, especially because they had already been humbled once and were earnestly trying their very best this time. What everyone had hoped to see was a tightly clustered band surrounding the estimate; ideally, between the nearest-neighbour Fibonacci numbers.
But when I looked at the data, I was deeply impressed by how good these estimates were. To me, the data shows that the devs had remarkably clear intuition about the tasks they were estimating, intuition that reflects their skill and experience.
The data had a strange regularity to it. Regardless of how long the estimate was, all of the graphs look… well… the same. If I removed the axis scale, you almost wouldn’t be able to tell which graph was which (except by the arbitrary bin sizes)4. When we normalize the measured completion time by the estimate, the distributions all were exactly the same. That means the developer’s estimate, while far from perfect, is also far from meaningless: it’s the scale parameter of some distribution.
And that’s not all…
A wild lognormal appears! It’s super effective!
Jaynes tells us that a probability distribution corresponds to a state of knowledge. What this investigation revealed was the exact state of knowledge that a skilled software developer has about a task that they have not started yet — something that the developers themselves weren’t able to consciously quantify. And while it is a long-tailed distribution, it proves to be remarkably consistent!
There are many long-tailed distributions that look similar to each other, but just one that fit the data suspiciously well, with suspiciously few parameters: the lognormal distribution. And not just any lognormal, but a particularly simple one, having a shape factor of 1 and a location parameter of 0. This lognormal distribution has only one adjustable parameter, the scale parameter m, which corresponds to the median, and is — quite remarkably — precisely the estimated completion time. And get this: the mean of this distribution just happens to be m times 1.6.
So here is the probability distribution for the time to complete a challenging software task, given that the developer’s estimated time is m:
What this study revealed was that when an experienced engineer thinks hard about a task and looks deep within themselves, drawing on their knowledge and familiarity with the work, they are really good at estimating the median completion time. Unbelievably good.
The only problem is, nobody is interested in median completion times!
Don’t tell me the probabilities; I just want a number!
As we’ve seen, estimates are fundamentally and unavoidably of type [probability distribution], but when we communicate or even reason about them ourselves, we tend to cast these estimates to type [simple number]. And this is a lossy compression: important nuance disappears. There’s no unique way to summarize a probability distribution with just one number, which leaves a lot of room for misunderstanding.
For example, I privately estimated that it would take four hours to write this article.5
My manager understands that estimates come with uncertainty. So does marketing. So do the customers even, usually. But everyone is looking for different things from an estimate, so when each one asks for “a number”, they want to be told different summary statistics of the same underlying probability distribution. Giving different answers to different questions isn't dishonesty, it's effective communication.
When marketing asks for an estimate, they want something they can commit to. They want to know the time by which, with 99% certainty, the product will be ready. If it's done sooner that's great, but that's not what they're asking. They want the 99th percentile. And that is what they think they are hearing, when they are told "four hours". It's not their fault; they asked for one number, and they got one number. At no point did anybody ever draw out the probability distribution to clarify whether they're discussing the same number.
On the other hand when a sprint manager asks for an estimate, they usually want the mean. They're assigning tasks to people, and people to tasks, and figuring out how much work can get done by the next sprint. If some tasks take longer than estimated and others less, that's fine as long as the errors tend to average out over a decently large number of tasks.
This chart gives us some quick, easy-to-remember rules for representing estimates as a single number, according to the risk tolerance of the conversation. Do they want accuracy, or do they want certainty?6
Of course, if you’re choosing a multiplier like this, you need to understand how the risks balance on both sides. There are some business situations where deals can be missed by being too conservative, and where delivering late might be easily forgiven. A factor of 10 would only be suitable when the risks are strongly one-sided. I’m showing you how to include risk tolerance in how you communicate an estimate, but it’s up to you to use your judgement about where those risks and rewards balance. Are you more afraid of missed deals, or missed deadlines?
How well does this generalize?
Is this result valid for all teams, and all projects? Probably not. If your task involves ordering hardware with a three-month leadtime from a vendor, then the lognormal might place way too much confidence on that task finishing ahead of schedule. And for repetitive and familiar tasks, completion time can be estimated with very good confidence. But for software projects involving some amount of novel exploration, where development efforts occur in-house by a highly skilled team, this seems like a very good starting point.
I wouldn’t speak so confidently except that I’m not the only one who has noticed this: This article was written after, and completely independently of, the internal study and analysis that I’m sharing here. I don’t think this result is coincidence; I’ve seen others report the same finding as well. Perhaps there’s a system at work?
The normal Gaussian distribution occurs everywhere in nature because of its high entropy and its ability to be generated by repeated application of simple random processes. The lognormal is likewise a simple high-entropy distribution, and it also has a simple mechanism for being generated in nature. I think this may shed some insight on how technology projects actually progress.
When a large number of random variables are added together, they will tend to converge on a normal Gaussian distribution. So we might expect that tasks, which tend to each be composed of several sub-tasks, would also have a Gaussian shape.
However, the lognormal emerges when random variables are not added but rather multiplied together.7 Often when you go to fix a bug or write a feature, the solution isn't straightforward. Sometimes you'll get it on your first try, but other times you have to come at it from two or three different angles before finding the answer. And then code review happens and you might need to make changes again. So completing a technical task can involve a "for" loop with a random number of iterations, which can quickly generate a lognormal curve.8
And sometimes, in the process of fixing something, you’ll encounter two or three other things that need to be fixed first, or find that the issue is the tip of a much bigger iceberg.
Management software like JIRA tends to classify work into a fixed number of distinctly-named levels like “epics” and “stories”, but if you actually draw out the entire list of work and the connections between tasks in any nontrivial project you will often find it more closely resembles a sort of fractal, with ever more fine-grained tasks the closer you care to look.9
The ubiquity of the lognormal distribution in technical work harmonizes with this view, and implies that beneath each task that you would attempt to undertake, you will find roots extending down to an unknown depth, and the only way to find out how far it goes is to get digging.
This post isn’t intended as professional engineering advice. If you are looking for professional engineering advice, please contact me with your requirements.
I’ve omitted or changed some minor details to respect the anonymity of the team and the company. I am sharing it with their permission.
This particular company had a rare combination of attributes that allowed for high quality data, including an unusual compensation structure and reporting requirements for tax credits, among other things. Time tracking was mostly accurate to 5 minutes; devs would sign out of work on a ticket to go to a meeting. The original data would certainly enhance this article and its message, but it is proprietary, so you’ll have to make do with these illustrations.
I should also clarify that this data is based on time actually spent working on the problem. If you are accustomed to making calendar estimates, you will need to correct for how much of your productive time will be applied to the task you’re estimating, and how much will not.
This optimism factor of 1.6 persisted even when developers consciously attempted to correct their estimates for it by taking Hofstader’s law into account.
While I’ve drawn histograms here to reflect how the data was actually presented at the time, histograms are usually not my preferred way of visualizing random data, because the (usually arbitrary) bin sizes can strongly influence how the results are percieved. You can display any numerical histogram more precisely as a cdf by sorting the data samples and then plotting their cumulative sum, which will look like something this:
If you really want to show the probability density, it would be the derivative of the cdf, which takes you right back to the raw data itself. Except the raw data is too noisy (which is why it was binned in the first place). Rather than binning it, which discards information, you’d be fully justified in applying a well-tuned smoothing filter to get a clearer look at the signal.
Four isn’t a Fibonacci number, but understanding the actual probability distribution behind an estimate is all that matters. Tricks like constraining yourself to the Fibonacci sequence add no additional value beyond that, just like the usefulness of rounding significant figures is superseded by providing actual error bars.
(By the way, it actually took twelve hours to write.)
By the way, why is the scaling factor 1.6 for the mean? Your mileage may vary but if you’re curious about the math, this lognormal distribution’s mean is larger than its median by a factor of exp(½), which is about 1.65.
Lognormals are also a pathological case where, as lognormals are added together, they remain almost-lognormal until a great many have been added, converging only very slowly to the normal distribution.
It’s rare to see anyone ever include “… and then we’ll likely have to try a second time” in a presentation to management, but the not-very-popular project planning framework known as GERT does allow for this.
I don’t know of any project management software that makes it easy to draw out these connections and properly link up all the hierarchical dependencies between tasks in a project. Because of the burden of documenting all those links, few teams ever get to see a whole project represented as one giant directed graph full of nested sub-tasks. Despite the effort required, it can be educational to try it once or twice on a big project, at least in retrospect, to learn what the real shape of technology work looks like, and why the schedule never plays out goes according to the Gantt chart.












> So completing a technical task can involve a "for" loop with a random number of iterations, which can quickly generate a lognormal curve
A for loop with random stuff would generate a normal
function getResult(){
result = 0
for (i=0, i<n, i++) {
result += get_random_factor(i)
}
return result
}
I think what would generate a lognormal is
function getResult2() {
result = 0
for(i=0, i<getDifficultyOfStage(0), i++){
for(i=0, i<getDifficultyOfStage(1), i++){
for(i=0, i<getDifficultyOfStage(2), i++){
for(i=0, i<getDifficultyOfStage(3), i++){
result += delta
}
}
}
}
}
return result
}
where the different stages correspond to e.g., solve problem, check with management, check with clients, fight upper management, etc etc.
Nice article. You have found a pattern quite similar to what I found comparing project estimates. When I researched further I found that this pattern was quite common. p10 at 1x, p50 at 2x, and p90 at 4x. Your pattern is a bit different as you have p50 at 1x and p90 at about 4x, but then I expect differences as you are at the task level and I measured at the project. As you say, lognormals add together and stay lognormal, but the standard deviation decreases. As tasks add up to be projects the range becomes smaller. As always one of the big challenges is that data is not readily available. Can you make the data available in some form?