Basics: Updating from data
A deep-dive
As a deep-dive, this article may be too long for email. If it does not display correctly in your inbox, please read it on the website.
In a previous post, I mentioned:
If your data is conclusive, the posterior will pin-point the right answer pretty quickly even if your prior was very broad to start with.
Let’s walk through an example just to see how this looks in practice.
The first example is called the lighthouse problem, and I’ll follow the presentation of D. S. Sivia, after Gull, in the book Data Analysis: A Bayesian Tutorial.
A lighthouse is somewhere off a piece of straight coastline at position α along the shore and a distance β out at sea. It emits a series of short highly collimated flashes at random intervals and hence at random azimuths. These pulses are intercepted on the coast by photo-detectors that only record the fact that a flash has occurred, but not the angle from which it came. N flashes so far have been recorded at positions {x₁…xₖ}. Where is the lighthouse?
I admit this sounds a lot more like math homework than a practical real-world situation. That’s probably because it is a math homework problem, from a Cambridge undergraduate problem sheet. Nobody actually tries to deduce the position of a lighthouse by littering a coastline with photodetectors. I hope you’ll let that slide because it’s actually very interesting, even if this situation bears a closer resemblance to the detective work performed in a neutrino observatory than by a maritime surveyor trying to track down their missing lighthouse.
Before we jump in and start crunching our data, let’s think for a second about what sort of data we would expect from this setup. We don’t know α and β, just the data xₖ. But often, the most effective approach to these situations is to flip things around twice: first, figure out what data we’d predict if we knew α and β, and then second, invert that relationship again to draw inferences from the data about α and β.
So, if we knew where the lighthouse was located, where would we expect to see the flashes?
Based on the description, the angle θₖ at which a flash is emitted from the lighthouse is always totally random. We have no reason to expect any one angle more than any other, so we expect a uniform distribution over the angles 0°-360°. Half of those flashes go out to sea, so really our distribution is over the ones that hit the coast, which will be (-90° to +90°) if we set 0° to be in line with the pier.
From basic trigonometry we then have:
Pretending that we know α and β, and with a uniform prior probability over θₖ, what should our probability distribution for xₖ be?
That is, given the above relationship and knowing that (θ < θₖ < θ + dθ | α, β, I) = dθ / π, what is (x < xₖ < x + dx | α, β, I)?
It takes a little bit of calculus, but we arrive at the following relationship:1
This is the Cauchy distribution, which at first glance looks a lot like a normal Gaussian bell curve, but with one important difference: it has very long tails. That’s not surprising; if the lighthouse throws out a flash almost parallel with the shore line, it’s going to go out a very long way, and the chance of that happening isn’t particularly small.
Although they look similar, the Cauchy distribution is sort of the exact opposite of normal. While the Gaussian curve has lots of nice properties, the Cauchy distribution is sometimes called “pathological” because of how mathematically troublesome it is. For example, you cannot compute the mean of it, nor its variance. The long tails on either side, which stretch out infinitely far in each direction, carry enough probability along with them that they prevent those calculations from converging.
(By the way, this means that an attempt to simply average all the data points xₖ together will never converge on the true value of α, no matter how much data we accumulate, because the outliers will keep throwing off the average).
So how should we deal with multiple data points, if not just averaging them together?
The data are independent, which means that the observation likelihoods simply multiply:
So now we need to flip this around again. We found what distribution of data we’d expect if we knew α and β. What α and β can we infer from our data? That is, knowing ({x₁…xₖ} | α, β, I), how can we find (α, β | {x₁…xₖ}, I)?
That’s where Bayes’ theorem comes in. Bayes’ theorem is what lets us invert a probability relationship:
We already found ( { x₁…xₖ } | α, β, I), so what we need is (α, β | I) and ( { x₁…xₖ } | I), and then we’re done.2 How do we get those?
(α, β | I) is our prior probability for the location of the lighthouse. If we had any clue where the lighthouse was to help guide our search for it, then this would be the place to use it. Is any location equally likely?
Not quite. β is a distance from the coast, and the problem description stated the lighthouse was off the coast (in the water somewhere). So β cannot be less than zero. This is a clue that β is a scale parameter, which means the fairest un-informative prior we can use is a uniform distribution over its logarithm,3 and so:
(Math teachers might hate it when we apply common sense to abstract homework problems, but we can also say that nobody builds lighthouses in deep-sea international waters, and use that to get a reasonable upper bound for β too; say, 100 km).
For α, the position along the coastline, there seems to be no particular reason to prefer any one location over any other. So a uniform prior best represents our knowledge:
(Assuming our coastline stretches only the extent of the local area and not the observable universe, we can bound this as well; say, 100 km in either direction. It doesn’t cost us much to extend those limits, so we can easily make them as long as we need, we just need to be generous enough that we don’t accidentally rule out the true lighthouse position. At the very least, whoever prepared the budget for these photodetectors ought to know how long the coastline is).
We don’t have any reason to think that knowing β tells us anything about α and vise-versa, so putting these two together, we have our prior for the lighthouse location:
Lastly, knowing nothing of α and β, symmetry suggests that (xₖ | I) should also be a uniform distribution over the coastline. After all, not knowing where the lighthouse is, we have no reason to expect any one photodetector to light up more often than any other. (In fact, ignorance of α would already be enough to drive that, even if we knew β).
Putting these priors all together and using the less verbose probability density notation, we get:
Lastly, the constant in this expression is whatever normalizes the probability; that is, to ensure it all adds up to 100%. We could work it out mathematically, but it’s easy enough to just add a normalization step in the computer program that we’ll be using at the end.
Now that we have our prior, and the distribution that predicts our observations, we finally have the expression that tells us, based on our data, where the lighthouse is:
Complicated-looking equations like this are fine as solutions to homework problems, but I just can’t feel satisfied until we’ve programmed this into a computer and have run it on some data.
Today, we’re going to do this brute-force style: evaluate the probability over an entire grid of possible locations, and see what “learning” looks like as we dial in the lighthouse location based on data.
The true location (drawn with a white circle on the area plot) is initially unknown, and that uncertainty is reflected in the width of the probability distribution. But as observations accumulate, the distribution gradually narrows and becomes more well-defined.
Source code is available on gitlab if you’d like to follow along.
In the next post in this series, we will see how closely we can match this Bayesian-learning ideal with much less computation by using a Kalman filter.
This post isn’t intended as professional engineering advice. If you are looking for professional engineering advice, please contact me with your requirements.
This is expressed in the notation that I described earlier, in which we always include a conditional on I to acknowledge the other information we have about the situation, besides the data and parameter values. For example, the problem description itself. This helps me avoid confusing myself by wondering the meaning of a probability that is conditioned on no information at all.
You might notice that I’ve changed my notation from (x < xₖ < x + dx | α, β, I), ie, “the probability that xₖ falls between x and x+dx given α, β, and the rest of our information”, to (xₖ | α, β, I), ie, “the probability of observing some data xₖ given α, β, and the rest of our information”. (xₖ | α, β, I) is obtained by taking the limit as dx→0. I’m using the latter as a shorthand and treating them as essentially equivalent concepts.
Technically speaking, though, the difference is that (x < xₖ < x + dx | α, β, I) expresses a probability (for some finite dx), whereas (xₖ | α, β, I) expresses a probability density. The distinction comes up when dealing with continuous probabilities. When you think about it, if our photodetectors are allowed to have infinite resolution, then the chance of observing xₖ in any precise location must be almost zero.
If we were dealing with discrete probabilities -- like if our shoreline's photodetectors were divided into individual pixels -- then (xₖ | α, β, I) would be a well-defined probability.
Some find this distinction a major sticking point, but as a general guide, if you ever find yourself getting conceptually stuck thinking about continuous probabilities, you can either unify the concepts with measure theory or as a shortcut you can use discrete probabilities for every step of a calculation. When it comes to running the data through a computer, you're probably going to end up discretizing variables into discrete values anyway, and thinking about how you would discretize a continuous probability (eg. dividing up a shoreline into finite photodetector pixels of equal size) can guide your thought process in the same way that measure theory would, helping you avoid confusion and calculation errors.
Likewise, (α, β | xₖ, I) represents a probability density over α, and β; to phrase it as a true probability, I would need to rewrite this as (a < α < a + da, b < β < b+db | xₖ, I). This expresses the probability that the true location of the lighthouse (α, β) lies within a square of area (db × da) about some point (a, b). It’s worth being clear about the conceptual distinction, especially to avoid confusing oneself between a true-but-unknown value (α, β) and a plausible candidate (a, b), but the probability expression is so notationally verbose that I will avoid using it unless really necessary.
This is known as a Jeffreys prior, and draws on considerations of transformation symmetry groups, which is often the best we can do when dealing with prior probabilities. But don’t worry; if you were to instead use a uniform prior over β, it might bias you toward thinking the lighthouse is farther out to sea than it probably is, but you’d eventually get the right results with enough data.










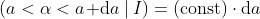

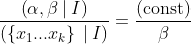

The jump from "a sample mean is useless" to a pdf of the possible location of the lighthouse is really cool. The discussion in the footnotes is very good. I'm now deep in Wikipedia