Better simulation can be the enemy of good design
"An approximate answer to the right question is worth a great deal more than a precise answer to the wrong question." - John Tukey
The progress of computing has delivered an entire arsenal of precise and wonderful tools into the hands of engineers. This includes finite element method modeling (FEM), Monte Carlo simulations, and now an ever-expanding toolbox of machine-learning frameworks and neural networks. Next to all this computational power, pen-and-paper analysis can start to look a little quaint and old-fashioned. I have met university students who wonder whether there’s now even any value in learning the “old ways”, especially when it takes so much time and effort to do so.
I’m not going to attempt a comprehensive defense of basic mathematics here, nor to dismiss the value of these amazing tools (which are amazing!). I’m just going to point out a particular, yet common, situation in which engineers may find themselves, and where a simple approach retains its value.
First, for the non-engineers in the audience, let me just explain what the finite-element method is. To put it a little too simply, it’s basically a general-purpose tool for numerically solving physics problems of almost unlimited complexity.1 A 3D model is meshed into discrete elements, and the laws of physics — solid or fluid mechanics, electromagnetism, thermodynamics, etc — evaluated over those mesh elements. Taken to the extreme, finite-element simulations can be (and are) made to simulate airplanes, fusion reactors, vehicle collisions, the atmosphere, or even the human body.
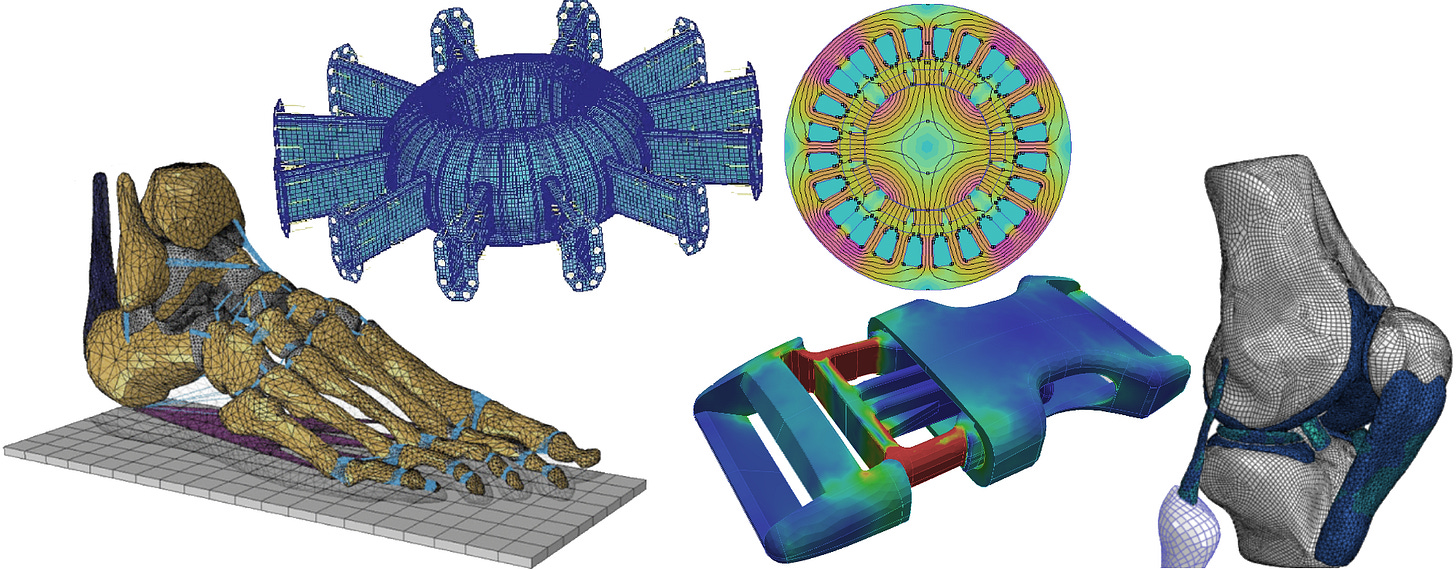
Finite-element simulations are still imperfect; they only yield approximate solutions, and depend on tabulated material properties or empirical surface-contact equations that don’t perfectly reflect reality. Still, when run by an expert, they can be very accurate and offer an extremely detailed picture that could never be matched even by the most intricately-instrumented laboratory experiment. Meanwhile, pen-and-paper analysis tends to offer solutions only for very simple equations on highly simplified geometries like lines, spheres, and planes. And while finite element software is not exactly famous for being user-friendly, neither is vector calculus. So for a student solving a problem, getting the computer to do all the work can seem like a route that is both better and easier.
… And it is the better route, for a certain class of problems, known as forward problems. These are questions in the form of “given precise scenario X, what is the precise outcome Y?”
For example, let’s say you have a certain make and model of car, and you want to find out what will happen if it crashes into a solid wall at a certain speed. Industry-standard finite element software packages like MADYMO and LS-DYNA can simulate this scenario with reasonably high fidelity. It’s not quite as representative as a real-world crash test perhaps, but on the plus side, you don’t destroy a car with every run. And there is simply no way that analytical methods will offer anywhere near the detail of this kind of computer simulation!
To be sure, it is dangerous to put too much trust in computer simulations just because they show convincing images with pretty colours. But those concerns can be surmounted by following best practices, and I’m not here to lecture about that.
What I’m talking about is their suitability for design problems. That is, “which scenario X will give us the desired outcome Y?”
Engineers encounter this kind of problem throughout their career (including every time a customer is disappointed by the outcome of their precisely-simulated crash test). Even when you know exactly how unacceptable the present performance is, there are a million things you might try changing to improve it. So what do you do?
This is where high-fidelity, compute-intensive tools like FEM are on shakier ground. It’s not that they can’t be helpful; they do have their place in the design process. But they shouldn’t take center stage, especially not early on during the prototyping stage.
There’s nothing wrong with accuracy per se. But model accuracy is mainly useful for forward problems. It’s far less important for design problems, where you should be more concerned with model generality.
Take friction modeling for example. High school physics students learn this equation for friction:
where μ is either the static or dynamic coefficient of friction, and Fₙ is the normal force. And… that’s about as much as you should ever need during design, unless you’re designing something whose core working principle revolves around intricacies of friction contact, like a stick-slip nanopositioner.
In fact, that equation is about as much as anyone who studies friction modeling can even agree on. If you want a model that precisely captures experimental results in detail, you’ll be picking from one of several nonlinear differential equations with multiple state variables and at least seven different parameters, depending on lubrication and surface roughness at various scales of interaction…
Computer simulation packages can capture this degree of nuance, when necessary, and if you’re trying to do a forensic reconstruction of a component failure, or debug your servomotor fine-motion control loop, you might well need it. But at the design stage, this degree of detailed physical fidelity isn’t just burdensome in terms of effort; there’s a very good reason why it makes things worse. That reason is: if your design’s success or failure hinges on the fidelity of your simulation, then you probably have not chosen a robust design.
Those viscoelastic friction parameters will change as soon as it rains, or when the temperature drops, or when it gets dusty, or when the contact surfaces have worn in a little bit. If you would let those simulation parameters alter your design decisions, ask yourself if you will also be controlling those parameters to that same degree when it’s running in the real world.
But before we get carried away, let’s look at this from another perspective. Design has a lot in common with optimization, so we can think about this like an optimization problem.2
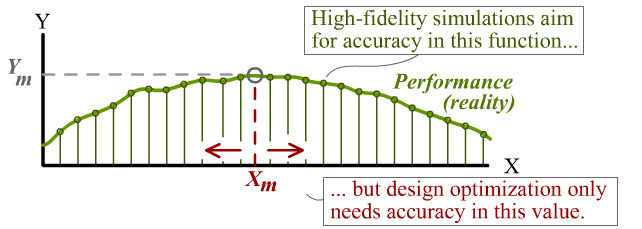
(The argument that follows is a bit abstract; if it helps to have a mental image as you read it, picture X being some design parameter like airplane wingspan, and Y being some performance metric like flight range.)
Forward problems are akin to evaluating an function, like Y = F(X). You probably wouldn’t be doing that if you didn’t care about knowing the true value of Y. Finite-element software can only offer an approximation, Y ≈ Fₐ(X), but it’s a very good approximation that’s tried its best to make Fₐ as close as possible to the true F for any point X.
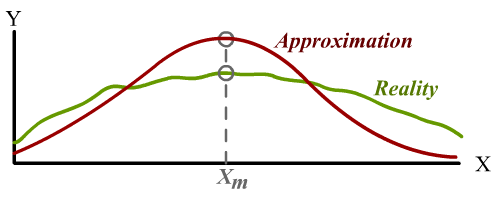
On the other hand, optimization problems are searching for the input (Xₘ) where the function reaches some maximum (Yₘ). And as students of calculus will recognize, this often doesn’t require you to accurately determine the value of Yₘ itself!3
For example, if your approximation has an error of the form of a vertical shift, or a scaling factor, that error will have no impact on Xₘ whatsoever! In fact, an approximation can be very unrealistic and yet still work well for design optimization, as long as it captures certain key trends and features of reality.4
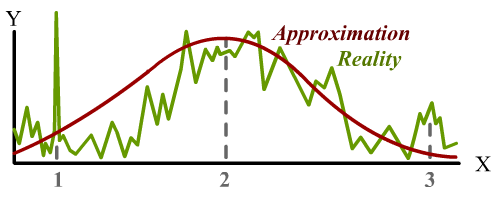
But the design process often benefits from using an approximation that deviates from reality. Reality tends to have a surprising amount of detail, but we might be better off if our models do not. In practice, finding Xₘ isn’t as simple as reading off a graph. A real design problem will tend to have many degrees of freedom, so it involves searching through a high-dimensional space. There are several ways to do this in practice, from numerical hill-climbing to genetic algorithms to symbolic calculus. What they have in common is that all of them benefit from the function being simple and smooth. Otherwise, we encounter this scenario:
Location 1 is technically the design that maximizes the performance metric, but it’s a narrow target in parameter space. Arguably, it is the “best” design. But not only will it be very hard for an optimization process to even find, we’ll also need to maintain very tight control of product tolerances in order to reap the benefits; any small deviation and the performance takes a plunge.5
Location 2 is where maximizing our approximation gets us. It’s not exactly the maximum of F, but it’s pretty good. Finding this point is also very easy, because of how smooth and well-behaved the approximation is; we can hill-climb from anywhere and reach this point.
Location 3 is a trap! It’s a design of middling performance, the top of a little hill of mediocrity. But many black-box optimization methods applied to F will tend to get stuck in these “local optima”. This is a major problem for optimization in general, which volumes of research has been dedicated to solving, all of which will tell you: if you can find a simple and smooth approximation, use that first.
When you need a robust design, one that works in an uncontrolled environment, you want to be aiming not for peaks, but for for plateaus.
Simple models generalize better, precisely because they lack fine detail.
And lastly, high-fidelity finite element simulations may be accurate, but they are not quick to evaluate. Even on a fast computer, a single iteration may take between one second and one hour.6 And if each simulation must cover an extended period of time (eg. a collision process) to check just one point in design-parameter-space, then that computation time starts creeping onto the calendar.
You certainly can brute-force it if you insist. I’ve seen companies lean on raw computing power applied in parallel to explore the design space, grinding through simulation after perfect simulation. And it can work, but it’s very limiting. The curse of dimensionality means that with a brute-force approach, no matter how much cloud compute you buy, you’ll be limited to exploring a small range of design parameters. If you just need to tweak the lamination thickness for an electric motor, go ahead, but if you’re starting from a blank sheet of paper, you’ll want a more effective method. Something to get you to that plateau right away.
This is where an understanding the physics of your problem is irreplaceable. Know how to find the scaling laws, the sensitive variables, the nondimensional parameters. And don’t forget: each parameter that you can find a closed-form expression for is one less dimension you have to worry about optimizing over. So please consider simpler, more approximate methods in the design stage, even if they’re not validated to industry standards, even if it’s video-game-quality ragdoll physics or spherical-cow-in-a-vacuum idealizations. You can still do that high-fidelity validation later, once you’ve found a design candidate to validate!
And engineering students, don’t abandon your coursework!
This post isn’t intended as professional engineering advice. If you are looking for professional engineering advice, please contact me with your requirements.
Technically, it solves problems that are described by linear or nonlinear partial differential equations; it just happens that partial differential equations are general enough to include almost any practical real-world physical scenario (although finite-element methods might not be the most efficient way to solve every problem, and there are other techniques such as finite-volume methods or multiscale techniques that are better for certain cases, but which I’ll group together here in one big bucket). Of course, running these simulations is subject to compute time and memory constraints as well; densely meshed models can get very slow, very quickly.
Also, while physical simulations are undoubtedly the main application, the finite-element method can of course be used to investigate all sorts of abstract non-physical scenarios with more than three dimensions or alternative laws of physics.
If you asked me the difference between design and optimization, I’d say that optimization involves iterating until your design is as good as you can get it, for some definition of “good”. But even when you don’t care about pushing cost or performance to the limit, design iterations are expensive and you often only get one shot to prove a concept. So design is a different sort of optimization, one where you take aim at the nebulous region of design-space where your confidence of success is highest, even if you have no data to go on yet.
I don’t want to throw out all nuance here; there’s value in finding Y too, of course. Once you’ve settled on design parameters that you guess are probably as good as you can hope for, you will still need to confirm how good that design is, because even an optimal design might not be good enough to solve your problem. But that just requires following up with a few high-fidelity verification steps; it doesn’t mean you need high-fidelity at every step along the way.
There’s actually a very broad class of transformations of F that don’t affect Xₘ. Try thinking of as many as you can!
“What if we include robustness to deviation itself in a new performance metric, and optimize that?” you ask. Very clever! This inherently smooths the space, and now you just have to turn the crank to maximize that function. But this is also an even-harder-to-compute function than the previous one, because evaluating it at any one point requires having estimated F at multiple surrounding points.
This wide range is really an understatement. It depends a lot on whether it’s a 2D or 3D geometry, the number of elements in the mesh, the equations being solved, and whether they are linear or nonlinear, the convergence threshold, whether you have institutional access to the world’s top three supercomputers, and so on. But regardless, it’s never a speed that would be mistaken for “fast” in an optimization process.


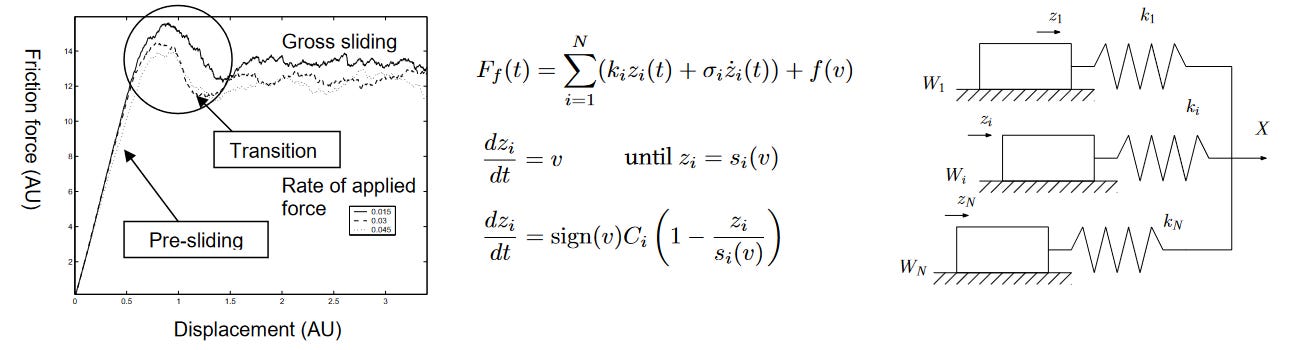
Great post! I was wondering if you have any thoughts on how topology optimization relates to these ideas.
It seems like topology optimization would be exactly the kind of tool you warn against using for a first pass at a design. It uses finite element simulations, the optimization problem tends to be pretty nonlinear, and even for the simplest problems, you’re optimizing over thousands of parameters.
The interesting thing is that depending on the design problem you’re applying it to, you can often get quick (minutes to hours) convergence to a robust solution. For example, maximizing the stiffness of a simply supported beam might yield this design (https://www.researchgate.net/profile/N-Olhoff/publication/226103134/figure/fig2/AS:302167828254721@1449053832660/figure-fig2_Q320.jpg), which could be found on a laptop in a few minutes (this one’s really simple). Of course we already knew that trusses made of triangles are good, but you can imagine how this would be useful for exploring design spaces that are harder to reason about.
Without being able to cite anything to support this, I feel like there are two perspectives in the literature. Some researchers want to use topology optimization to create fully-formed designs, which would be realized with 3D printing or maybe a 5-axis mill. But others present it as a tool for finding the initial guess, which you would then refine using other techniques. That second perspective seems at odds with your argument.