Chaos control!
An unpredictable system is not necessarily an uncontrollable one.
Author’s note: I still have several prerequisite posts to be written explaining some of the basics that I draw on here. I apologize to anyone who feels like they’re being dropped in the deep end. But on the other hand, sometimes jumping in the deep end helps us appreciate the basics.
Chaos. Control. Surely these are two things that do not mix? Aren’t chaotic systems the epitome of the uncontrollable?
Well, in this article we’ll see how chaos can not only be controlled, it can even be levered to improve control.
Although chaos had already been discovered by the 19th century in the context of a physics problem (the “three body problem”), those findings mostly didn’t permeate the wider physics and engineering community until the mid-20th century. By that point, the quantum physics revolution had already shaken the mainstream belief in a predictable, deterministic, “clockwork” universe that had dominated since Newton’s era. Nonetheless it still came as a shock to realize that even a clockwork universe might still be unpredictable. After all, quantum weirdness could be swept under a carpet, affecting microscopic objects only, while the familiar world of macroscopic objects still obeyed familiar clockwork rules.
When even the best clockwork around — electronic computers — started behaving chaotically, it became hard to ignore. Edward Lorenz famously stumbled over this problem while studying thermal convection in the atmosphere. Lorenz noticed that computer simulations diverged into dramatically different trajectories despite nearly identical initial conditions. Lorenz’s equations were describing a chaotic dynamical system. This was the famous and serendipitous discovery of the butterfly effect, a story that has been told many times and much better than I can recount in this article. Veritasium has a great presentation here.
Formally known as “sensitivity to initial conditions”, the butterfly effect is the notion that a mere butterfly flapping its wings could steer the path of a tornado halfway around the world. It’s a fascinating and inexorable property of chaotic systems, and it’s more than just a poetic notion; it’s literally true.1
Usually when the butterfly effect comes up in philosophical conversation, it’s used as a warning about the futility of trying to understand complex systems, or the limitations of linear thinking. Believing you can control a chaotic system is pure hubris and next thing you know dinosaurs are eating your customers. Right?
So let’s look at Lorenz’s system, and then we’ll see what happens when we try to control it.
“The lack of humility before nature that’s being displayed here… staggers me.”
— Jeff Goldblum, as chaos theorist Ian Malcolm (Jurrasic Park)
Lorenz and his colleague Barry Saltzman were developing a mathematical model for thermally-driven convection in a gas, as a small step toward understanding the atmosphere. As sunlight warms the ground, the air heats up; warm air is less dense than cool air, so it rises upward toward the stratosphere, where heat is released; colder air displaced from above circulates back downward to replace it. The hope was that this might reveal a way to predict the weather. It’s simple physics, but right from the start there are reasons to expect interesting behaviour.2
Lorenz identified three interacting degrees of freedom in this system:
the circulation velocity,
the temperature difference between the updraft and downdraft, and
the skew of the temperature trend along the vertical axis.3
Let’s call these variables x₁, x₂, and x₃. Left to its own devices, this system evolves according to the following nonlinear differential equations (don’t worry, you won’t be asked to solve them):
Let’s set these equations in motion and watch what happens. This part might look familiar if you’ve already been introduced to chaos theory.
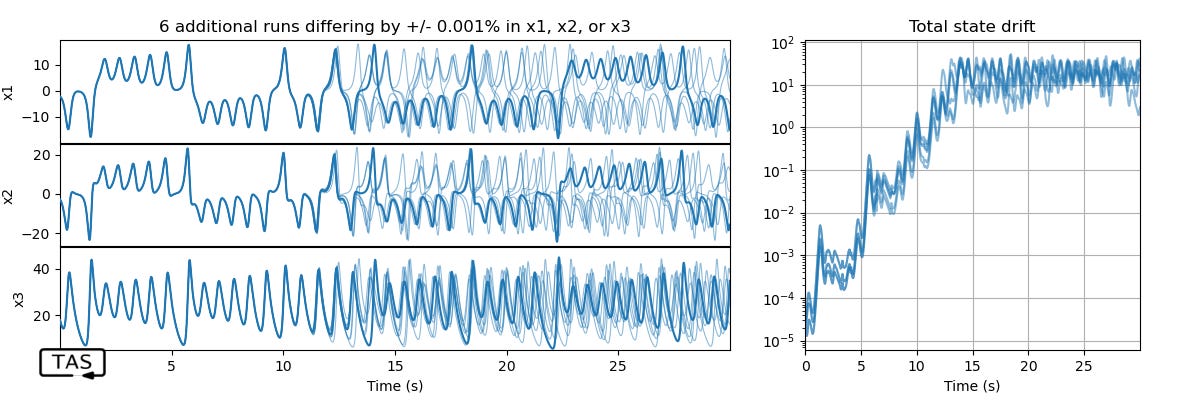
There’s quite an irregular pattern among all three variables. It’s almost hypnotizing to watch; it never stops, never repeats. And the best is yet to come. What happens if we change the system state by just a tiny amount — say, out by 0.001% in just a single state? It’s hard to see at at first, but…
Over time, the trajectories grow apart exponentially. That’s the butterfly effect.4
Since there are three state variables, we can visualize the system state as a point in a three-dimensional space where each coordinate represents the value of one of the state variables.5 As the system evolves over time, the point moves and traces out a curve.
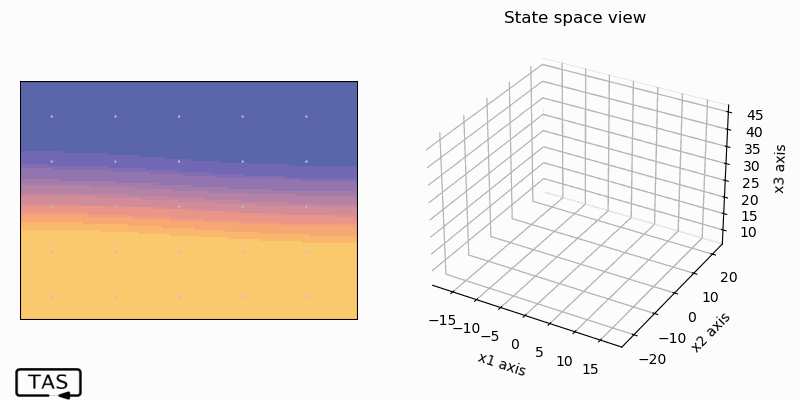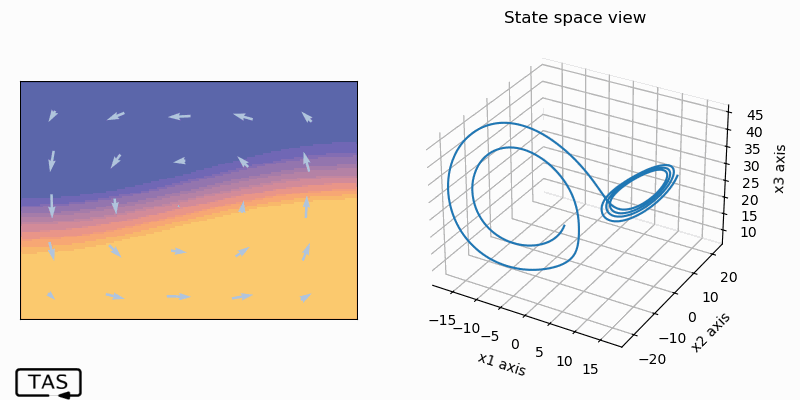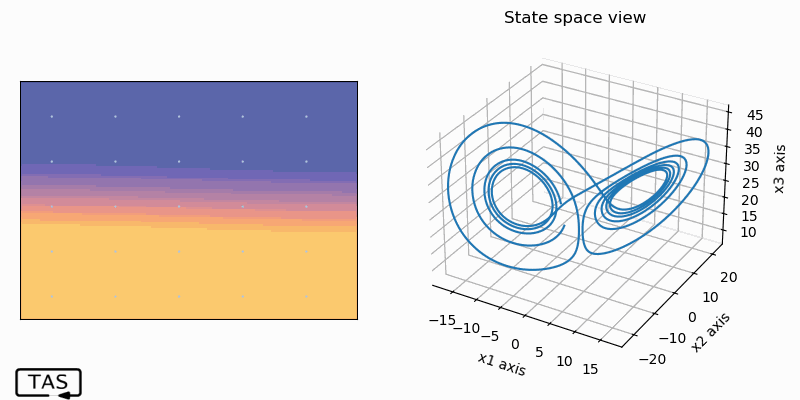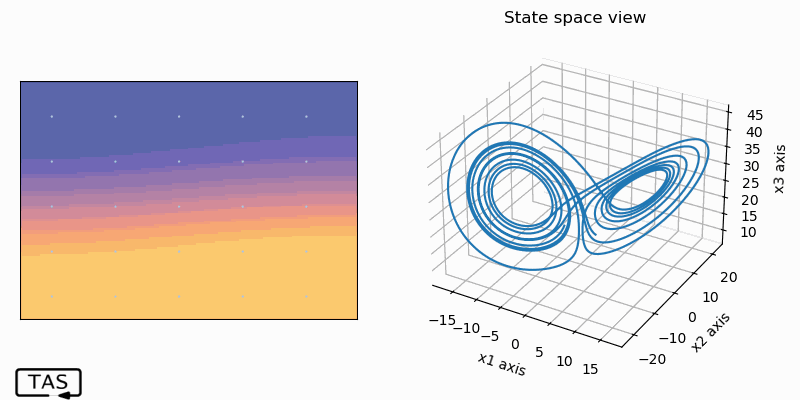
Although this system is chaotic, it’s still deterministic. At each point in this space, the equations of motion describe which adjacent point the system will to move to next. So the state at any one time completely determines the future trajectory. And if you think about it for a while, you’ll realize that this also means that if a trajectory ever returns to any state that it’s ever been to in the past, then it will go on to retrace the same path through state-space it did the previous time.6 The motion would be periodic. For the motion to be aperiodic, the curve must never intersect itself.
It just so happens that paths that are close together don’t stay close together for long. So if you aren’t sure of precisely where you’re standing, then you can’t be sure which path you’re walking down. In fact, if you want to predict the state far into the future, there’s no sufficiently-small error that you could get away with. You need to know the exact state. And since all measurement has finite precision, we can never know the exact state of any real system.7
So, would you believe this chaos can be controlled?
Some apparently find it hard to believe.
Would you believe it can be controlled with linear feedback on just a single state variable?
Let’s take a look.
First of all, I admit we have to sort of twist the problem a little here. In order to have any chance of controlling a system we need at least some kind of input that we can adjust, and as described by Lorenz, the system has no inputs at all; it just evolves completely autonomously. We need to introduce some kind of actuator.
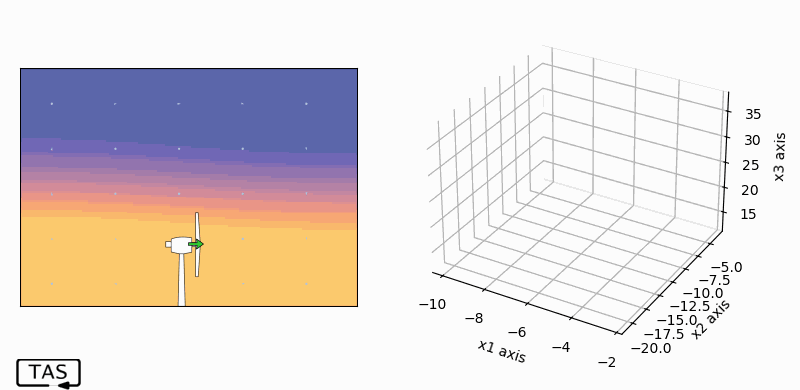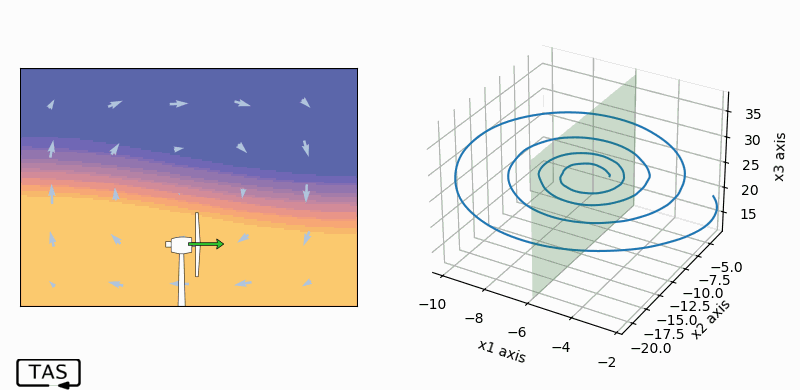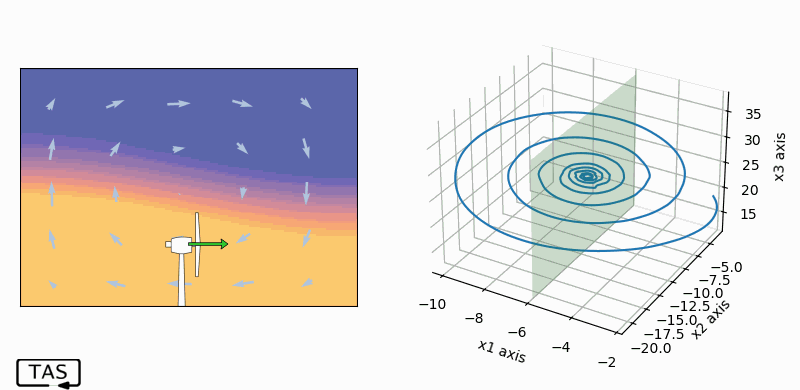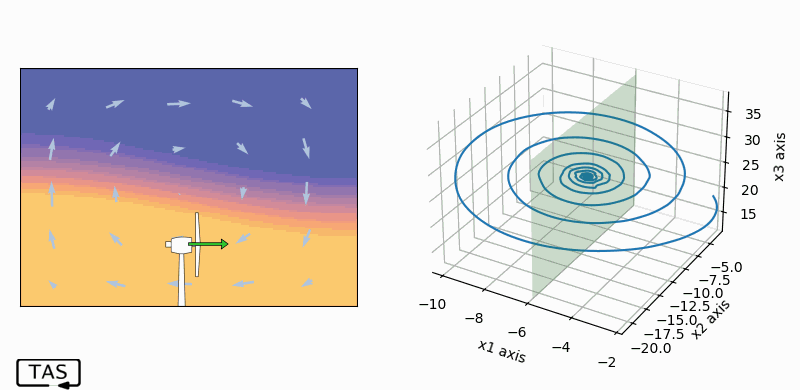
There are a few options, but the one that’s easiest to visualize would be to put a little fan on the ground which can blow left or right, adding or subtracting a little velocity to the circulation motion. This adds a new term to the system’s differential equations.
And for good measure, let’s put in a sensor that can detect the circulation velocity, so that our fan can adjust its behaviour to whatever the system is doing wrong. Now we’re ready to test feedback control. Let’s start with the old proportional control trick.
And here’s the result:
Well…! Isn’t that interesting!
Not only did we stabilize the fluid velocity, we stabilized both temperature gradients along with it, and we weren’t controlling them or even measuring them. The whole thing is in equilibrium. In fact, the chaos has completely disappeared from our system!
And — I didn’t mention this, but I’ve even set it up so that the velocity sensor is quite noisy, so the measurement error is much higher than the 0.001% error of the previous simulation. Even though this system is very sensitive to small changes of state, and the controller has only a vague idea of what the exact state is, it works anyway. The sensitivity hardly seems to matter.
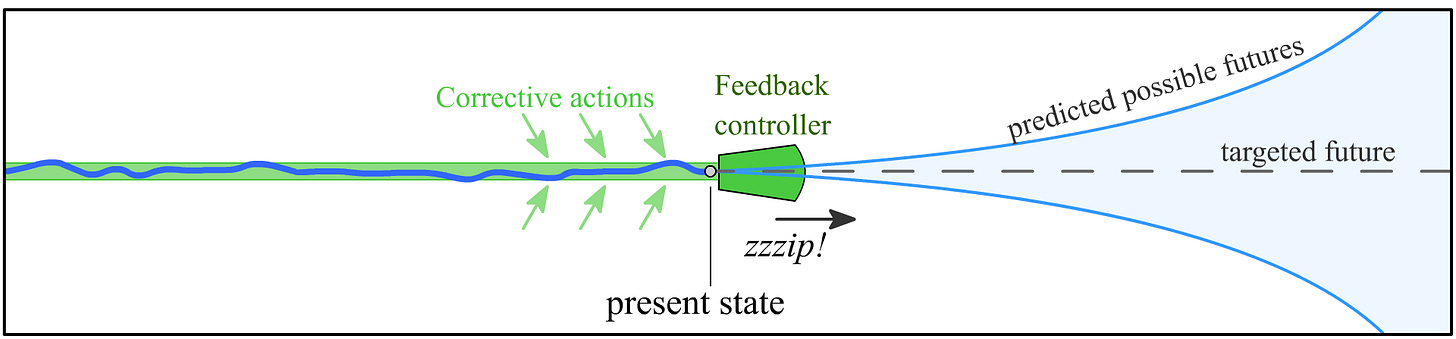
This is one of the points I’d like you to take away from this article. Controlling the long-term evolution of a system is different, and in many ways easier than, predicting that long-term evolution.
The key is that our controller doesn’t have to decide all of its future actions up-front; it will be able to make use of additional information as time goes on. We don’t need to be able to predict where the system’s current state will carry it in the long term, or know the current state to infinite precision, as long as we can get frequent measurements that keep the controller up-to-date on deviations.
(But the controller can — and should — react to future information according to set rules. That’s the difference between ‘a control algorithm’ and ‘flying by the seat of your pants’.)
And while our system is chaotic and sensitive to small changes in state, it takes time for the trajectory to veer off-course. As long as the controller reacts quickly enough, it can maintain authority.
At each instant, looking toward the future, there’s an exponentially-growing cloud of uncertainty about what the system might do. But like a closing zipper, as time moves forward and we get new measurements, that cloud of uncertainty shrinks. The constant intake of sensory information cancels out the entropy of chaos, and the corrective control action ensures that the system state doesn’t stray too far from the intended track.
But even so, we’re only measuring one variable. Why did the other two start to behave?
Two bare-minimum requirements8 for a system to have the aperiodic motion typical of chaos are:
it needs to be non-linear, and
its state-space needs to be at least three-dimensional.
The reason for the latter requirement will be familiar to anyone who has played the computer game ‘snake’, in which you play as an ever-growing snake who has to navigate a field without ever crashing into your own tail. Remember, if the system’s trajectory in state-space ever crosses itself, then it is forever trapped in a periodic orbit. If you draw a line on paper without ever lifting the pen, you’ll eventually trap yourself. But if you can move the pen in 3D, it’s very easy to keep going forever.
OK. So, by stabilizing one of the three parameters, we’ve now removed X as a variable and constrained the three-dimensional Lorenz system to a two-dimensional plane. The chaos necessarily disappears. It would still be conceivable for them to oscillate periodically amongst themselves, but for the Lorenz system, even oscillation would require the system trajectory to move off the plane that our controller has constrained it to.9 So by controlling just one parameter, all three variables get trapped at the same time, like they’re stuck to flypaper.
Proportional feedback is still pretty rudimentary control, even though it worked this time. I can’t really say the system is even under control yet; it’s merely settled in an equilibrium. Can the controller get smarter? The Lorenz system is rich enough that one could devote a doctoral thesis to perfecting its control, but here I’ll just sketch out a rough idea of how I’d tackle this problem quickly.
What I love about linear systems is that if a control algorithm works anywhere, then it will work everywhere, in any state of the system.10 For a nonlinear system that is no longer the case; the dynamics of the system change depending on which region of state-space it’s occupying at the moment, and the controller either has to adapt its behaviour or else just be robust enough to handle the full range. It takes much more care and testing to guarantee that the controller will never go haywire, because each test is only valid for its conditions.
Still, a good feedback controller only has to work for small deviations about a target point (even if that target moves around). Many nonlinear systems have locally linear dynamics, including chaotic systems, and the Lorenz system is no exception. At any given point in state-space we can analyze the dynamics of the system as though it were linear. Let’s look at the frequency spectrum and pole-zero locations of the Lorenz system’s local linear approximation, over a range of convection velocities x₁, and the (unmeasured) thermal states x₂ and x₃. I’ll just plot them all together:
Quite a diversity of behaviours, isn’t it? Resonances pop up, change frequency, and disappear; the low-frequency gain varies by orders of magnitude; the system is often unstable or nonminimum phase… But at an immediate glance, we can also see some order among the chaos. In the high-frequency domain, around 50 rad/s and higher, the spectrum converges to a single line, a first-order rolloff, and that’s our opportunity. This tells me that a single, appropriately-designed PI controller can handle the full entire spectrum of behaviours, and do it very well, so we don’t need to resort to gain-scheduling or other nonlinear controller designs.11 Furthermore we can basically read the required controller parameters right off the plot, so no trial-and-error tuning is required.

Of course, in order for this approach to work, we will need a control bandwidth of at least 100 Hz — unstable systems demand fast reflexes, after all.
With this higher-performance controller in place, we can not only stabilize the system, we can also cleanly follow a moving target:
And here’s the closed-loop transfer function. That tangled mess has become well behaved and much more tightly-clustered, almost like a single linear system, thanks to the magic of feedback. It goes to show that you don’t always need a nonlinear controller to control a nonlinear system.12
(I hope I wasn’t out of line throwing those Bode plots at you.13)
So far I haven’t specified any physical limit on the output of the control actuator, but now let’s imagine that our fan can only exert a very weak influence on this system. Think of large-scale systems like… well, the motion of the atmosphere, which has a total driving power on the order of 1000 TW, which is about 50 times the entire combined power harnessed by human civilization. Even if that system were well-behaved and linear, we couldn’t expect to control it using a tiny little fan.
But as it turns out, the fact that a system is chaotic can sometimes be used to our advantage in such situations. How does that work?
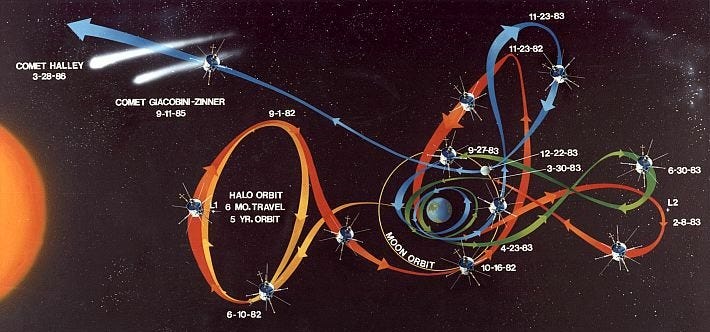
A common goal in control is that you want to bring your system to a certain desired target state. Chaotic systems have this nice property called topological mixing which means that, left to its own devices, the system’s trajectory will trace out pretty much the entire space of accessible configurations, eventually coming arbitrarily close to any desired state. Furthermore, sensitivity to initial conditions means that a small perturbation from any state can radically alter the natural trajectory. So rather than use brute force, you can wait for opportunities to apply small, carefully-planned influences to guide the future state in favourable directions, keep it on track using feedback, and once it’s close to the target, just gently hold it in place.14 It’s a strategy that requires patience, however.
As it happens, this is exactly how NASA elegantly repurposed its ISEE-3 spacecraft to do a flyby of two comets with minimal propellant.
So nonlinear systems, even chaotic ones, can often be controlled. Even though any tiny deviation can completely alter the long-term evolution of the system, feedback control makes up for that by constantly observing the system and reacting to changes in real time.
Does this mean that the government is running a secret project to control the weather using wind farms?
Well, I’d still find that very hard to believe.15
This post isn’t intended as professional engineering advice. If you are looking for professional engineering advice, please contact me with your requirements.
There are many phrasings of the butterfly effect, and some are truer than others. A more common presentation is “the flap of a butterfly’s wings could cause a hurricane halfway around the world”, and this is on weaker ground. Even chaotic systems are still bound by the laws of physics, including conservation of energy and momentum. A small disturbance will, over a span of time, put the system trajectory into a very different part of phase-space, but it will still be restricted to the same energy hypersurface. A butterfly’s wing flap doesn’t add nearly a hurricane’s worth of energy all on its own.
And yet, there’s still a sense in which even this weaker version is true. Energy from the sun is constantly being added to the Earth’s oceans and atmosphere and stored in various forms. As this chaotic system evolves, its trajectory will sometimes pass near a critical threshold, like a ball rolling almost to the top of a hill, just barely unable to make it over the top. At those points that built-up energy is on a hairpin trigger, and even a tiny deviation is all it takes to release it in the form of a hurricane. So while the butterfly’s wing-flap isn’t causing the hurricane all on its own, the butterfly effect can make the difference between a hurricane happening or not happening. However, in this case the butterfly is only altering the timing of the hurricane; even without the wing-flap, that energy would inevitably have been released at a different opportunity. This is a consequence of topological mixing.
Also, the butterfly effect is not instantaneous. It takes time for small change in conditions to manifest itself as a large deviation in the system’s trajectory, and the smaller the initial disturbance, the longer it takes. It might be thousands or millions of years before the butterfly’s wing-flap results in a deviation on any significant scale. But the first butterflies evolved around 40 million years ago, and by now we’re probably seeing the effects of those wing flaps.
There are also some deeper philosophical objections to the butterfly effect, like “if we’re treating the entire atmosphere as a deterministic system governed by differential equations, then surely so is the butterfly itself, so there’s no counterfactual world in which the butterfly didn’t flap its wings. Why are we acting like the butterfly’s wing-flap is some exogenous input to the system? We may just as well say that the tornado randomly decided to turn left”. Or, “events can have more than one cause, and between a butterfly and a helicopter, the helicopter is a little higher up on the blame list”. Fair enough.
One reason to think this might be interesting is because fluid motion is always full of surprises. The Lorenz system is a special case of the Navier-Stokes equations, famous for their complexity. As Heisenberg said, “When I meet God, I am going to ask him two questions: why relativity? And why turbulence? I really believe he will have an answer for the first.”
But Lorenz’s chaos is not caused by turbulent motion; his model doesn’t have enough degrees of freedom to include the small vortices that are a core feature of turbulence.
There’s another reason: even before we’ve built a model, we can see that some kind of symmetry-breaking bifurcation will be necessary. Air at the bottom has to move up, air from the top has to move down, but they have to somehow agree on a direction in order to stay out of each other’s way and form a convection cell. Unless the mathematical model includes some kind of built-in asymmetry like a slope of the ground, every direction looks the same at every position, so there’s no reason for the fluid to move in any particular way. Because of this symmetry, there is indeed a valid solution to the equations where the air remains perfectly still, with warm air on the bottom and cold air at the top. As it happens, when the temperature difference is small relative to viscous drag, this solution is stable; as the temperature gradient gets larger, this solution remains valid but it is unstable, needing only the smallest disturbance to set the fluid in motion. This ratio is called the Rayleigh number, and when this number crosses a certain threshold the system goes from calm to agitated.
So you can see why this problem was of interest to atmospheric scientists. The surprising part, though, is that once the fluid does get set circulating in a certain way, it doesn’t stay that way; it never settles into a repeating pattern.
By the way, this is still a highly simplified model. It doesn’t capture a lot of the interesting physics that drive the weather, such as humidity and condensation, Coriolis forces, and so on.
Lorenz’s model assumes the floor and ceiling temperatures are both held constant, which means that the average linear temperature gradient is also fixed as (T₂ - T₁)/H. But over that distance the average temperature could vary as a straight line, or most of the temperature change could happen near the top or bottom, or it could even reach its most extreme temperature somewhere in the middle.* It’s not quite as easy to visualize, but that’s what this third parameter describes: the “bend” rather than the “slope” of temperature. It’s the second-order temperature gradient (or the second-harmonic in a Fourier series).
* (Because heat always flows from hot to cold, the temperature reaching its hottest or coldest value somewhere far from the top or bottom surfaces would be… thermodynamically curious, unless it were part of the initial conditions. So we should expect this temperature-curvature parameter to remain within certain limits as the system evolves over time. On the other hand, the model is a simplification so some departure from reality is expected.)
At least, they grow apart exponentially for a while. The rate of divergence of the system states is quantified by the Lyapunov exponent. Eventually they’ve drifted as far apart as they possibly can within the accessible state-space, and the distance saturates into a flat line (with random fluctuations).
(Note: A linear slope on a log scale signifies exponential growth).
By the way, exponential divergence from a tiny initial error is not unique to chaotic systems. Unstable linear systems do the same thing. The difference is that chaotic systems diverge while the state remains bounded, and without converging back to any other stable point or cycle.
It’s a 3-dimensional space, but the three axes are not the familiar (x, y, z) dimensions. This space is called “state space” because the coordinates specify the state of the system. It’s also called “phase space”, especially in the physics community, a name that somehow seems more appropriate for periodic motion.
That is, as long as the system is time-independent. But I personally view every time-dependent system as just a bigger time-independent system in disguise. (And if you continue along this line of reasoning, it’s not long before you start doubting the existence of time itself.)
Even if you somehow did know the exact state of the system, your simulation would still eventually diverge from reality due to numerical rounding error, which introduce tiny deviations in each step. (Unless, of course, the system you’re trying to simulate is another computer running the same calculation with the same rounding.)
Note that these are not the defining properties of chaotic systems (and there are a few different definitions in practice). These are just certain basic requirements that can be inferred by the Poincaré–Bendixson theorem (subject to certain requirements that the Lorenz system satisfies, like continuity and boundedness).
For completeness’ sake, a commonly-used definition of chaos requires:
dense periodic orbits,
topological mixing, and
sensitivity to initial conditions (although this might be implied by the first two).
The first one is kind of an interesting, paradoxical property: it says that chaotic systems are filled with periodic trajectories. And yet despite this, you barely ever encounter them in practice for any random initial conditions. I’m trying to stay out of the weeds here, so that’s a subject for another day…
You might also be wondering, what if a 2D trajectory follows a space-filling curve? The ultimate solution to the game of snake, it’s an infinite curve that packs in a finite area and never needs to self-intersect. Could that allow chaotic or aperiodic motion from a second-order nonlinear system? The answer is… well, I’m actually not sure; this calls for a pro mathematician! But just going by intuition, it’s very hard for me to imagine that a continuous-time dynamical system whose trajectory was a space-filling curve — if that is even possible — could ever have its state evolve by a finite radius in a finite time, given that the length of such a curve is infinite.
By the way, just like at least 3 dimensions are needed for chaos, at least 2 dimensions are needed for oscillation. First-order systems, with just a single state variable cannot oscillate. (At least in the continuous-time case; for discrete-time systems there are counterexamples, but real discrete-time systems are hard to find outside of a computer.) This is one reason for the effectiveness of sliding mode control, although there’s a caveat there big enough to deserve its own article. (Sliding-mode systems aren’t actually 1D).
Also, just to be clear: it’s the state-space that needs to be at least 3-dimensional. The system can still be moving in two physical dimensions. The Lorenz system itself is constrained to a plane by its symmetry. A chaotic double-pendulum moves in a plane, but its state-space is four-dimensional (two angles and two velocities).
But the converse is also true: if a linear system is unstable, then it is unstable everywhere, and that’s usually trouble. By contrast, an unstable nonlinear system can shift into a new equilibrium where it becomes stable again. That’s not necessarily an equilibrium state that you want, but it’s the one you get. Sometimes. Depending on the nonlinear system.
In this case, the simple proportional controller will not stabilize all possible states of the Lorenz system, but it doesn’t have to; the system will bounce out of the unstable ones until it settles in a state which does stabilize. With an unstable linear system there would be no such luck.
As a general preference, unless there’s very good reason, I prefer feedforward controllers to be nonlinear, and feedback controllers to be linear (or at least very simple). It’s not always possible, and even PID controllers have nonlinearities, but there are two reasons to keep feedback linear: (1) if the feedforward is doing a good job and the reference trajectory respects physical limits, the feedback controller will only ever be reacting to small errors, so linearity is usually sufficient, and (2) feedback control always introduces the potential for instability, so it’s more important to be safe and predictable, rather than make the problem worse.
Hysteresis / sliding-mode controllers of course are an exception (because despite being nonlinear they are also very predictable).
The system has become more linear in the sense that the system’s dynamics are less sensitive to the system’s state.
In fact, this is one of the reasons feedback control was developed in the first place. For example, in 1927 the telecom industry was running on vacuum-tube amplifiers, which suffered from statistical variation and a wide range of undesired nonlinear behaviours, resulting in distortion and cross-talk in the telephone signal. Electrical engineer Harold Black realized that by applying negative feedback, the vacuum tubes could be made to behave much more predictably, linearly, and uniformly, and over a wider bandwidth.
Still, the job’s not done yet; if this were a critical application rather than a blog post, I’d want to explore the performance limits of this controller over a wide range of states, look for bifurcations, and be able to make more bulletproof guarantees on its stability, at least for operating points of interest. We could also look at attempting to infer the unmeasured states from the measured one, or developing a MIMO (multiple-input, multiple-output) controller. And of course, I’d want to add a feed-forward controller to improve the trajectory following even further. But this post is getting long enough, so let’s leave it there.
I know this audience has a diverse background, many of whom won’t be familiar with such tools, and I haven’t written an introductory article yet to introduce them. If those don’t mean anything to you and you feel like you’re being dropped in the deep end of the pool, I apologize — but I hope the underlying message is still accessible.
I also hope that this might provide some motivation to learn the tools of linear systems theory, or at least gain some intuition for them. Despite the relative simplicity of linear systems, it’s a subject that takes a lot of work to master, and many people lose motivation believing those tools won’t be useful with nonlinear systems. So take this as an example!
Some states will be easier to sustain than others. The closer the state is to an equilibrium point (whether stable or unstable), the weaker the actuator you can get away with. In other cases we can stabilize an orbit, rather than a static equilibrium. For more details, see The Control of Chaos: Theory and Applications by Boccaletti et al.
By the way, you might be wondering how you can know which way to nudge the system, given that the long-term evolution is unpredictable. While this is true, continuous measurement and feedback are again the keys here. Chaotic systems are frequently balancing on knife-edges, and so they’re difficult to predict when you can’t foresee which way they’ll roll. But given the opportunity to measure and push one way or the other, you don’t need to have perfect foresight. The trick is to set the feedback controller’s reference trajectory to match the simulation’s prediction: now the system is constrained to evolve the way you expected it to, and the feedback “effort” (eg. propellant) required to accomplish this will be kept small, because the reference trajectory is surfing the natural dynamics of the unforced system.
With sincere apologies to anyone who hasn’t seen the classic Get Smart.
(But in all seriousness: no. The high-frequency convergence that the Lorenz system shows does not exist in a real fluid-motion system, because the Lorenz equations neglect higher-order whirls and eddies in the fluid motion which will occupy those higher frequencies.)




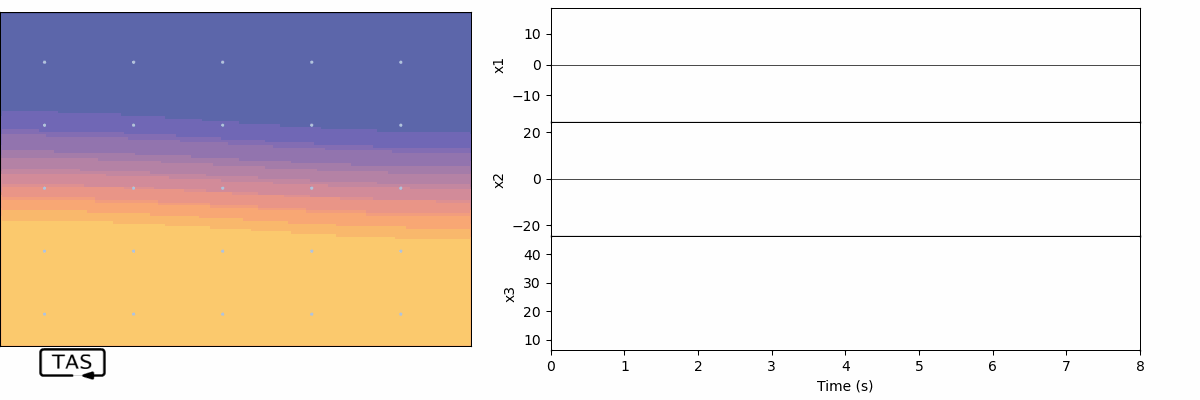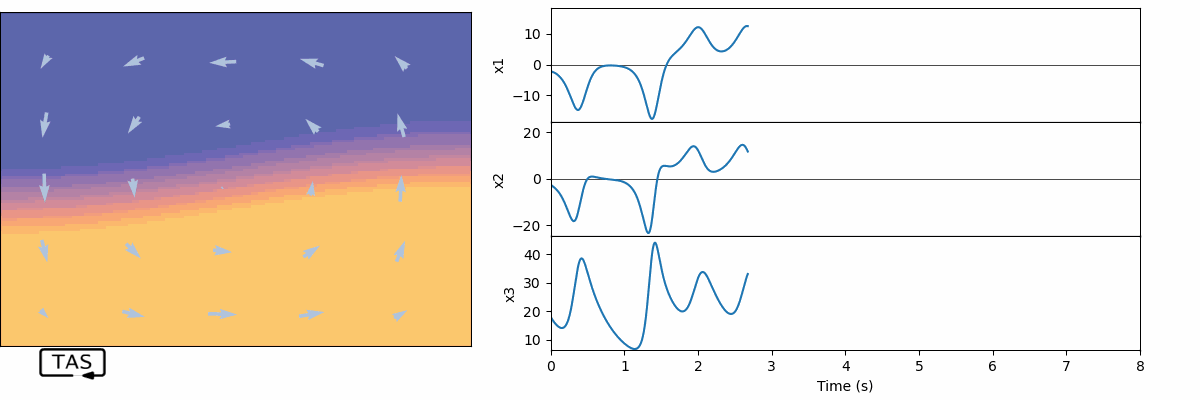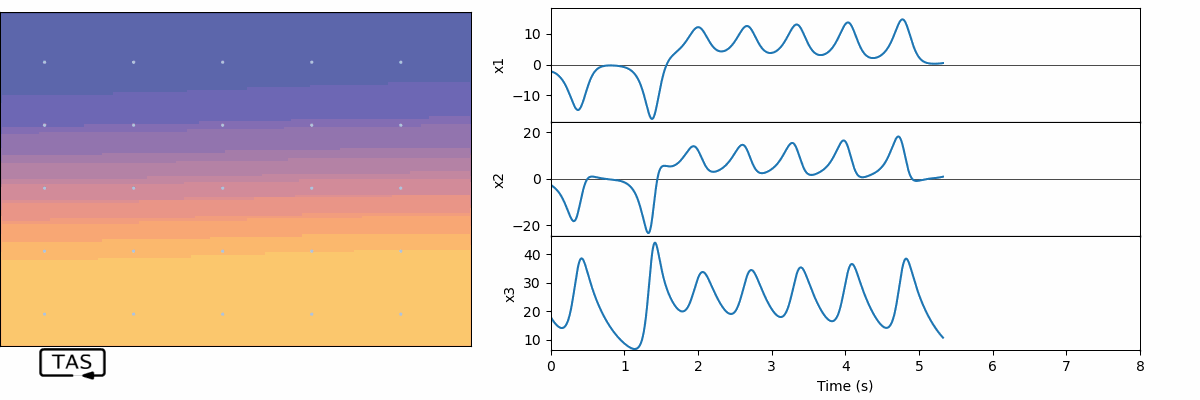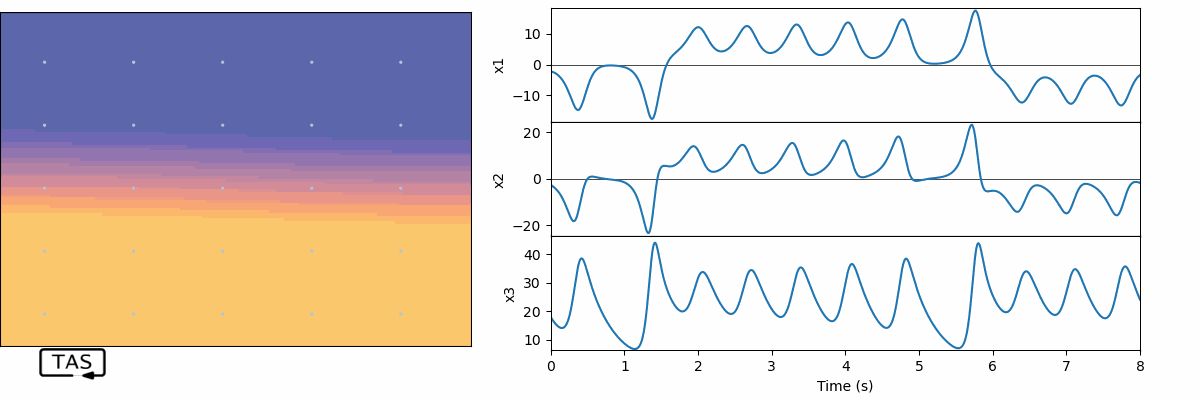






I'm reminded of random number generators. Designing them seems to be a dark art, but one thing they try to do is to maximize the period. Eventually every finite state machine must repeat, but by having a long period, they put that off as long as possible.
From: https://www.pcg-random.org/rng-basics.html
> A pseudo-random number generator is like a big codebook. In fact, a 32-bit generator with a period of 2^32 is like a codebook that is 16 GB in size, which is larger than the compressed download for the whole of Wikipedia. But a 32-bit generator with a period of 2^64 is like 64 EiB (exbibytes), or about six times a mid-1999 estimate of the information content of all human knowledge. How big would an actual book of 2^64 random numbers be? It would be so large, it would require the entire biomass of planet earth to make!
> One difference from a spy's codebook is that in a typical random generator everyone has the book. Thus, whereas spies would keep their codebook secret and could allow anyone to know the page number, random number generators do the opposite—the sequence of the generator (the codebook in our analogy) is known, but if we want to avoid prediction, no one must know where in that sequence we are looking. If the sequence is large enough (and there is no discernible pattern to the numbers), it will be infeasible to figure out what numbers are coming next.
Also, if you have a large enough state space and a clever design, you can set up a random number generator to generate Shakespeare:
From: https://www.pcg-random.org/party-tricks.html
> An argument for k-dimensional equidistribution goes like this: Suppose you bought a lottery ticket every week—how would you feel if you discovered that the clerk at the store was handing you a fake ticket and pocketing the money because, at 259 million to one, you were never going to win anyway. You might, rightly, feel cheated. Thus as unlikely as any particular k-tuple might be, we ought to have a real chance, however remote, of producing it.
> An argument against providing k-dimensional equidistribution (for large k) is that infinitesimal probabilities aren't worth worrying about. You probably aren't going to win the lottery, and your monkeys won't write Shakespeare.
> But what if rather than blindly search for Shakespeare, we manufacture a generator that is just on the cusp of producing it. [...]
God may not play dice, but she does play billiards.
Fantastic article, I'm going to come back and savor it.