Is the Kalman filter a low-pass filter? Sometimes!
Quick notes: No, These Are Systems isn’t going to be just “the Kalman Filter Blog”. Yes, I plan to continue the inflation series. Yes, I am still planning to write an introductory series about control theory more broadly. There’s a lot of material to get through! As always, I welcome your feedback.

Among the frequently-asked, frequently-unanswered questions about the Kalman filter are these:
Is the Kalman filter essentially a kind of frequency filter, like a low-pass filter?
Do Kalman and low-pass filters serve the same purpose?
Which one is… better?
Ahh, the never-ending war between the time-domain and the frequency-domain perspectives. Well, let’s get some answers!
My previous two posts in this series introduced the idea of Kalman filtering, and examined how it relates to the principles of Bayesian probability. (If the term is new to you, then read those first!)
To quickly summarize: a Kalman filter is a very fast, very effective algorithm that you can use for estimating the true value of some signal in the presence of noise. (Among other applications).1
But to anyone with signal processing experience, that sounds immediately reminiscent of the job of a frequency-selective filter, such as a low-pass, high-pass, or band-pass filter. In fact, pretty much the first thing anybody does when they notice their data is too noisy is to reach for some sort of low-pass filter to clean it up a little.
(To bring you up to speed, a low-pass filter is any technique that smooths a signal by cutting out high-frequency noise. A simple version that many readers will be familiar with is running a moving average in Excel.)2
So is the Kalman filter a sort of frequency filter?
The question is actually a bit more complicated than it sounds, because there isn’t any one Kalman filter. The Kalman filter is really a recipe for constructing optimal linear predictive filters, but the actual characteristics of the resulting filter will depend on the dynamics, state variables, and sensors that you’ve tuned it for, and that dependence gets reflected numerically in the various matrices that your specific Kalman filter is built from.
And nor is there any one frequency filter.
A low-pass filter might nicely smooth out the noise from a sensor, but if you’re trying to tune into an FM radio station, it wouldn’t be the right choice — you need a bandpass filter, centered on that station’s frequency.3 On the other hand, if you want to remove trends to look at short-term cycles in the housing market, then you’ll want a high-pass filter.4
The frequency-domain view suggests that we think in terms of signal and noise occupying various parts of the frequency spectrum, and sometimes competing with each other. The frequency filter that is right for you depends on what counts as signal to you, and what counts as noise.
Not surprisingly, there is also a recipe to construct optimal frequency-domain filters, given some prior information about the spectral densities of the signal and noise, respectively. (This is called the Wiener filter, after the “Father of Cybernetics” Norbert Wiener).5 6
Wiener’s recipe is famously difficult to work with, but basically says: “let through such frequency bands where the signal exceeds the noise; cut out those where the noise exceeds the signal.”
Well? Are they the same? Stop explaining why it’s so complicated and just answer the question!
Okay, okay.
Let’s look at an example: a temperature sensor measuring a cup of water that is exposed to the elements. (Let’s say this is part of a remote weather station). The water temperature T gradually drifts up and down, unpredictably influenced by the surrounding environment in ways that we can’t predict, because we’re not measuring the surroundings — just the water. In the time between one measurement Tₖ and the next, the water temperature will have drifted by some mean-square amount Q, although we can’t predict in any individual timestep whether that drift will be big, small, or even up or down.
On top of the real changes in water temperature, the sensor also adds its own measurement noise with variance R. And to keep things simple, it’s all Gaussian white noise.
The corresponding Kalman filter for this system has a very simple 1D structure, so we don’t need any matrices:
Prediction step:
͞μₖ = μₖ₋₁ — We don’t know which way the system will move next
͞σ²ₖ = σ²ₖ₋₁ + Q — Our certainty about the future is less than the present
Update step:
Kₖ = ͞σ²ₖ/( ͞σ²ₖ + R) — Kalman gain tracks measurement confidence
μₖ = ͞μₖ + Kₖ(Tₖ − ͞μₖ) — Mean belief shifts with surprising7 new data
σ²ₖ = (1 − Kₖ) ͞σ²ₖ — Uncertainty shrinks with the new data
You might notice that regardless of what the measurements Tₖ actually are, the variance σ² evolves exactly the same way with each update: Average down towards R, and then grow by Q; average down towards R, then grow by Q again; etc. After the filter has been running for a while, the variance — and thus the Kalman gain — approaches a steady state:8
What do I mean by “a while”? Let me show you:
At this point, the recursion relationship for the mean from one update to the next becomes a linear filter with constant coefficients:
As it happens, this is precisely a first-order low-pass filter with a pole at z = 1 - Kₛₛ. We can plot this on a Bode plot, which displays how a system transforms signals of various frequencies. (Have you ever seen the Bode plot of a Kalman filter before?)9
And here’s what both filters look like in action. The Kalman and Wiener filter outputs overlap to the point that it’s quite difficult to distinguish them. (I gave them both an initial guess that’s off by 5°C).
Remember, filtering data isn’t just about smoothing your measurements to make them look nice for your boss. A good filter gives you the best estimate of the truth from measurements that are corrupted by noise.
So in summary: yes, at least for this system where using a low-pass filter is justified, the Kalman filter becomes that low-pass filter, after it’s been running for a while.
And indeed, it turns out in general that as the Kalman filter runs, it gradually morphs into the optimal Wiener filter for the system it models.10 11
Source code is available on gitlab if you’d like to play with this.
In fact, in his famous 1960 paper, Rudolf Kálmán introduces his filter partly as a technique for constructing the optimal Wiener filter. And in that paper, he makes the very same observation:
x*(t + 1|t) = Φ*(t + 1; t)x*(t|t – 1) + ∆*(t)y(t) (21)
The dynamic system (21) is, in general, nonstationary. This is due to two things: (1) The time dependence of Φ(t + 1; t) and M(t); (2) the fact that the estimation starts at t = t₀ and improves as more data are accumulated. If Φ, M are constants, it can be shown that (21) becomes a stationary dynamic system in the limit t → ∞. This is the case treated by the classical Wiener theory.
— R. E. Kálmán, A New Approach to Linear Filtering and Prediction Problems
In other words, if the covariance is initialized with its steady-state value, and the noise and system dynamics don’t vary with time, then the Kalman filter is a conventional frequency-domain filter with constant coefficients.
So does that mean the Kalman filter is better than the best frequency-domain filter?
If you care about rapid convergence to truth from an initial state of broad ignorance, or if you’re dealing with a system whose dynamics or noise characteristics are themselves evolving in some way, then the full (ie, dynamic) Kalman filter is much better equipped to deal with that.
On the other hand, if you’re going to be processing the same signal continuously, or you can initialize to a known-correct state, then implementing your filter as a dynamic Kalman filter is both overkill and wasteful, because you’ll just end up inverting a bunch of matrices every timestep for no reason. For such cases, it makes a lot of sense to precalculate the steady-state Kalman gain and then implement a Wiener filter with constant coefficients. And as a plus, this will allow you to leverage the powerful techniques of frequency-domain analysis like poles, zeros, and Bode plots to guarantee that your system stays well-behaved.
So I’m not going to declare a victor here.
This post isn’t intended as professional engineering advice. If you are looking for professional engineering advice, please contact me with your requirements.
Other applications of the Kalman filter include parameter estimation, state prediction, and sensor fusion. Some of these can be accomplished with frequency filters as well, although it can take some head scratching to apply them effectively. By contrast the Kalman filter comes “batteries included” for such applications.
A moving average filter is when you clean up a noisy signal by averaging together each n adjacent values. Most people who work with data in spreadsheets have done this at least once to clean up a graph.
Technically speaking, the moving average filter is a type of low-pass finite-impulse-response (FIR) filter, which means that when an input signal drops to 0 after time t, the filtered output signal will also decay to 0 after some finite time t + τ. FIR low-pass filters, by their construction, have all their poles at z = 0. FIR filters are popular for various reasons, but mainly because they are straightforward to customize, numerically well-behaved, and always stable.
More generally, low-pass filters can also be of the infinite-impulse response (IIR) variety, which are allowed to have poles placed at finite frequencies. These can have powerful performance advantages, but require a bit more care in their design.
That said, it’s not simple to make bandpass filters that are both highly selective and highly tunable. A common technique is to use a superheterodyne receiver, which starts with a broad-spectrum bandpass filter, then mixes the signal down to a lower frequency (usually 10.7 MHz) via a tunable oscillator, and then applies a second, highly selective, fixed bandpass filter at 10.7 MHz to extract just the radio station you want to listen to.
By the way, every microphone — including your ear — is constructed with a built-in mechanical high-pass filter to null out slow pressure variations across the membrane so it only captures acoustic vibrations, rather than acting as a barometer. In your ear, that role is played by the Eustachian tube.
Although in accordance with Stigler’s law, the Wiener filter may have been originally discovered by Andrey Kolmogorov.
Cybernetics is a fascinating field relating to the intersection of control theory, feedback, communications, psychology, and AI. In some respects it lies somewhere between an engineering discipline and a philosophy. It’s perhaps fallen out of favour these days, but I think it deserves more attention. You could even say that These Are Systems is an attempt to look at the world through a cybernetics lens.
By “surprising”, I mean that the farther the new data is from your expectations, the more it causes you to update your beliefs.
The Kalman filter “recipe” doesn’t specify how the covariance should be initialized (that’s up to your prior information to decide). If you initialize the covariance with this steady-state value, it will of course reach this condition instantly.
I plan to write a followup post on how we can go back and forth between a code-ready function like this one, and its frequency spectrum. Stay tuned.
This doesn’t only go for low-pass filters. The optimal Wiener filter for a system will take on whatever spectral shape is necessary, whether it be a low-pass, band-pass, high-pass, band-stop, or arbitrarily complicated filter mixing characteristics of all of these. It all depends on the characteristics of the system that the filter is being optimized for. And the Kalman filter will converge to that same filter, too.
Technically, there are a lot of different “Wiener filters” too, and I’m deliberately simplifying things. The Kalman filter converges to the discrete-time IIR Wiener filter, which is to say, the best kind of Wiener filter. :) There are also FIR Wiener filters, which are perhaps more commonly encountered. (But I’m already digressing too much).






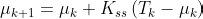


Hey Jacob!! I was scouring the internet for this exact article, and lo-and-behold it's written by the legend I used to work with (you derived a lead-lag controller on a whiteboard when I was a co-op student off the top of your head). Thank you for the awesome read. I was thinking of trying to replace a low-pass butterworth filter with a kalman filter in a system with no known inputs but lots of disturbances and measurement noise, just like the example you chose. The discrete math is going over my head for now, I've been relying on diagrams and python state space / simulation libraries to give me my answers so far, but will be implementing it in a more real-time fashion soon and will definitely be referencing your article!
Good series of articles.
In recent years, Ive moved from Kalman to Sav Golay filters, which in many circumstances work as well but are computationally much simpler. They also have a few additional 'tricks' such as providing the first & second differential signal.
We use such filters in motion control applications.